LEY DE LENZ
La ley de Lenz para el campo electromagnético relaciona cambios producidos en el campo eléctrico en un conductor con la variación de flujo magnético en dicho conductor, y afirma que las tensiones o voltajes inducidos sobre un conductor y los campos eléctricos asociados son de un sentido tal que se oponen a la variación del flujo magnético que las induce.
La polaridad de una tensión inducida es tal, que tiende a producir una corriente, cuyo campo magnético se opone siempre a las variaciones del campo existente producido por la corriente original.
El flujo de un campo magnético uniforme a través de un circuito plano viene dado por:
donde:
= Flujo magnético. La unidad en el SI es el weber (Wb).
= Inducción magnética. La unidad en el SI es el tesla (T).
= Superficie definida por el conductor.
= Ángulo que forman el vector perpendicular a la superficie definida por el conductor y la dirección del campo.
Si el conductor está en movimiento el valor del flujo será:
A su vez, el valor del flujo puede variar debido a un cambio en el valor del campo magnético:
LEY DE FARADAY
La ley de inducción electromagnética de Faraday establece que el voltaje inducido en un circuito cerrado es directamente proporcional a la rapidez con que cambia en el tiempo el flujo magnético que atraviesa una superficie cualquiera con el circuito como borde:
Donde 
es el campo eléctrico, 
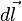es el elemento infinitesimal del contorno C, 
es la densidad de campo magnético y Ses una superficie arbitraria, cuyo borde es C. Las direcciones del contorno C y de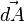 
están dadas por la regla de la mano derecha
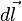es el campo eléctrico, es el elemento infinitesimal del contorno C, es la densidad de campo magnético y Ses una superficie arbitraria, cuyo borde es C. Las direcciones del contorno C y de 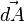están dadas por la regla de la mano derecha
Esta ley fue formulada a partir de los experimentos que Michael Faraday realizó en 1831. Esta ley tiene importantes aplicaciones en la generación de electricidad.
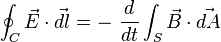
Exelente we
ResponderEliminar